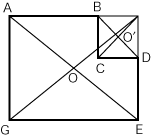
（解法その３）この図形が大きな四角形から小さい四角形を切り取ったと考えるのです。もとの大きな四角形の中心をOとし、切り取った四角形の中心をＯ’とします。OとO'を直線で結びます。この直線（図示していません）が図形の面積を２等分しています。

（説明）Oを通る直線は必ずもとの大きな四角形の面積Sを２等分しています。もとの大きな四角形に注目すると、OO'の直線で分けられた下の方の面積はS/2となっています。同様に切り取られた四角形の面積をS'とします。切り取られた四角形に注目すると、OO'で分けられた下の方の面積はS'/2となっています。したがって、直線OO'から下の部分の図形の面積は(S/2) - (S'/2) = (S - S')/2となっていて、全体の面積S-S'を２等分していることになります。