パズル
ここでは今までに集めた面白いパズルや、自作のパズルを紹介します。その前にぜひとも紹介したい人がいます。知る人ぞ知るマーティン・ガードナー (Martin Gardner1914年10月21日 - 2010年5月22日) です。アメリカの数学者、著述家、アマチュア手品師。懐疑者であり、疑似科学や超常現象批判でも有名。サイエンティフィック・アメリカン (Scientific American) 誌上で25年に渡って連載したコラム、『数学ゲーム』 (Mathematical Games) で著名。数多くのパズルに関する本が出版されています。パズルがお好きな人は(すでにご存知でしょうが)ぜひこの人の本をお読みください。
(7)ケーブルの対応付け
ある家の1階と2階に7本のケーブルが通っています。それらは同じ形をしているので見分けることが出来ませんし、途中は家のなかを通っているのでどれがどれに対応しているか分からない状態になっています。これらのケーブルの対応付けをしたいのです。
使える道具は導通の有無を調べるテスター(持ち運びはできます。テスターのコードは短くて一階と二階の間は届きません)だけです。つまり、一階にある7本のケーブルにA、B、C、....Gというラベルを貼り、それに対応した2階の7本のケーブルにも1,2,3,....7というラベルを貼り、その対応表(例えばA=6、B=2...など)を作ることが目的です。
例えば、1階にいるときにラベルA以外の6本のケーブルの端を一緒にして導線でつないでおいて、2階に行って、テスターで調べると1本だけ導通がないケーブルを見つけることが出来ます。それにラベル1を貼れば、A=1という対応が出来たことになります。このようにして何回か1階と2階を往復すれば、すべてのケーブルの対応付けができますが、効率的ではありません。
一回だけ往復して、すべてのケーブルの対応付けをする方法を見つけて下さい。これがこのクイズです。あなたは今一階にいます。2階に一度だけ行ってから1階に戻ってきて対応付けを完成したいのです。どうすればよいでしょう。一階(または二階)にいるときはどんなに時間をかけて導通の有無を調べてもかまいませんし、ラベルも自由に貼って下さい。最終的にラベルの対応表が完成すればよいのです。
(6)文字列のパズル
なんとかJasonというDJ ( FMとAMラジオのディスク・ジョッキー)の名刺に下記の様に書かれていた。あいにく、最初の一文字が消えていた(四角で表示してある)。この文字列に隠されているある法則を見つけて、この人のファーストネームの頭文字(英語のアルファベット1文字)を見つけて下さい。
ヒント:ピリオドとダッシュ記号は無視する。大文字と小文字の区別も無視する(全部大文字扱いと考えて下さい)。
![]()
(5)数字のパズル
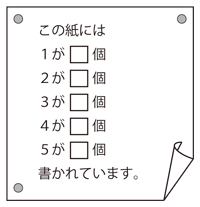
これは小学生から大人まで楽しめる(?)パズルです。「下図の紙の中の四角内を数字で埋めなさい。」というのが問題です。四角内の数字も数としてカウントされます。例えば、1が1個とすると、この紙には1が2個書かれていることになりダメです。解は一通りです。高校の数学の先生に出題しましたが、頭を抱えていました。かえって小中学生のほうが楽に解いてしまうかも知れません。答えはこちら。
(4)キャスト・パズル(市販品)
知恵の輪みたいなやつで、もっとうんとむずかしいものです。一つ1000円位で本屋さんなどに売っています。難易度のランクが1から6まであり、特にランク6は難しいです。私はランク6は6つ持っていますが、やはり一番難しいのはCAST QUARTETです。エルクは2ピースなので、少し動かしていると解法がみつかりますし、ニューズも試行錯誤を繰り返せば外れるでしょう。先日知人の5歳の坊やにニューズを渡したらあっと言う間に外されてしまいました。ただしちょっとした仕掛けがあるので、外れたらじっくりと仕組みを調べてから元に戻さないと、再度外すのが困難になります。このホームページ( http://www.hanayamatoys.co.jp/product/pazzle/cast.html )で見てください。
パズルがあまり得意でない人はランク1〜3などから始めたほうが無難かと思います。知恵の輪が嫌いな人はやめたほうが良いかもしれません、イライラしますよ。しかもこのシリーズには解答がのっていません。多分外せなくてそのまま燃えないゴミになってしまった人もいると思います。
実はこのシリーズを監修している芦ヶ原氏は2004年6月に胃癌で亡くなっています。以前に友人と一緒に氏の自宅を訪ねて、収集品などを見たり、説明を聞いたりしたことがあります。パズルの収集家/研究家としてはとても有名な人でした。
(3)等面積切断パズル(私のオリジナルパズルです)
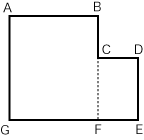
問)下のように長方形ABFGと(それより小さい)長方形CDEFが下の辺を合わせて合体した図形ABCDEGがあります(点線は補助線)。さて、この図形の面積を二分するように切断したいのですが、その切断直線を求めて下さい。使えるのは定規(線をひくだけで、寸法は測れない)と鉛筆だけ。1本はすぐ分かると思いますが、実はもう2本ひけます。図形の形によっては3本引けない場合(2本が重なってしまう場合とか、切断すると3つに分かれてしまう場合)もあります。(図の場合は3本引けます)。2本は比較的簡単に求められますが、残りの1本を引くのが難しいかも知れません。
(2)切符パズル
切符に印刷された4つの数字全部を使って、四則演算だけを用いて10を作ることから発展したパズルです。
(A)4つの4をすべて用いて、1から9までを作ってください。但し用いてよいのは四則演算(と括弧)だけ。よく切符に書かれた4桁の数字を四則演算(加減乗除)だけ用いて10を作るパズルと同じです。例えば(4/4)+(4/4)は2になります。このようにして、1,2(これは今作りました)、3,・・・・と9まで作ってください。ちなみに10は作れません。この問題は小学生高学年でも(括弧が入っている整数の四則演算ができれば)解けます。答えはこちら。
(B)1,1,9,9の4つの数字すべてを使って10を作ってください。ルールは上と同じ。これは上よりむずかしいです。作るのは10だけです。これは私が大学生の時に友達から出されて苦しんだパズルです。この問題は中学生以上が対象です。 答えはこちら。
(C)1,3,4,6の4つの数字すべてを使って24を作ってください。ルールは上と同じ。これは上よりさらにむずかしいです。
この問題も中学生以上が対象です。 答えはこちら。
(1)5円玉のパズル
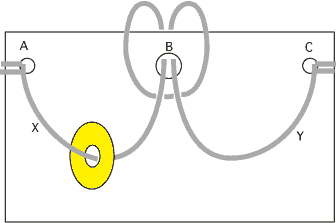
次図のように板にA, B, C の穴を開けてヒモ(途中がたるむように長めにする...図よりもう少し長めがよい)を図のように通します。ヒモのX の部分(A とB の間の部分)に5円玉を通しておき、両端は穴A, C に結んでおきます。穴B はヒモは通れるが、5円玉は通れない大きさ(5円玉の穴より少し大きめがよい)にしておきます。さらに板の上にもX, Y などという名前を書いておきます。
ここで、問題です。ヒモのX の部分にある5円玉をY の部分(B とC の間)に移動してください。勿論ヒモの両端を外してはいけません。板の上にX, Y などと書いておかないと、移動したか分からなくなりますので、書いておいてください。あるいはYの方にも5円玉を通しておき、どちらかの5円玉を移動して2つを一緒にさせてもいいでしょう。ヒモはタコ糸とかビニールひも等ではなく、しなやかな太めのヒモが扱いやすく、パズルらしいです(当然5円玉の穴より細くなくてはいけません)。ヒモの長さはある程度余裕が必要です。